Prova scritta di Fisica – Modulo II – CdL in BIOTECNOLOGIE
AA 2000/2001 – 5 luglio 2001
Prof. G. Sartorelli – Dott. M. Selvi

COMPITO A

Esercizio 1

Effettuando 100 esperimenti di conteggi di un certo fenomeno fisico vengono misurati i seguenti valori.

Numero di conteggi : n	1	2	3	4	5	6
Volte osservate: n	10	17	24	23	15	11

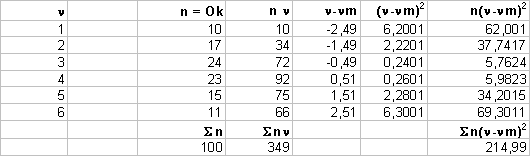
a) calcolate la media e la dev. standard dei dati ottenuti

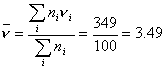
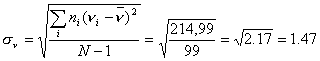
calcolate i valori di aspettazione in ogni intervallo nell’ipotesi che i dati seguano

b) una distribuzione di Gauss (scegliete il numero di conteggi n come valore centrale dell’intervallo)

non avendo a disposizione le tabelle, si deve procedere in modo approssimato ricordando che la probabilità in ogni intervallo è uguale all’area sotto la curva, delimitata dalla curva stessa (la gaussiana, in questo caso) e dagli estremi dell’intervallo. La possiamo approssimare con un rettangolo avente:

altezza pari al valore della Gaussiana, con parametri X e s ricavati dai dati al punto precedente, al centro dell’intervallo

base pari alla larghezza dell’intervallo, cioè 1.

Dopodichè occorre moltiplicare la probabilità ottenuta per il numero di eventi totali (100)

c) una distribuzione di Poisson

è sufficiente ricavarsi i valori della probabilità in ogni intervallo, usando la definizione della distribuzione di Poisson e moltiplicare per il numero totale di eventi

Si ottiene

d) valutate quantitativamente quale delle due ipotesi è più probabile. Quale parametro dovete confrontare?

Per sapere quanto bene una distribuzione si adatta ad una ipotesi teorica utilizziamo il test chi-quadro.

Minore è il valore ottenuto, migliore è l’adattamento

Bisogna confrontare, però, il valore del chi-quadro ridotto. Infatti esso è indipendente dai vincoli, che sono diversi nelle due distribuzioni ipotizzate. Il confronto del semplice chi-quadro non sarebbe completamente corretto.

Vediamo l’ipotesi di Poisson

I vincoli sono due: la media (calcolata dai dati) e il numero totale di eventi.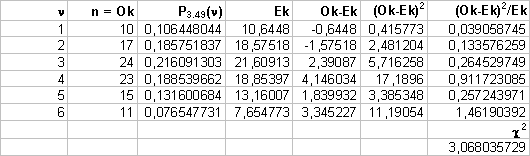

I gradi di libertà, quindi, sono:

d=n-c=6-2=4

E il chi-quadro ridotto vale: 3.07/4=0.78

Per l’ipotesi gaussiana:

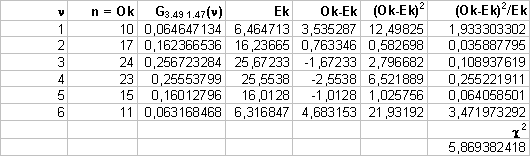
I vincoli sono tre: la media e la deviazione standard (calcolate dai dati) e il numero totale di eventi.

I gradi di libertà pertanto sono:

d=n-c=6-3=3

Il chi-quadro ridotto vale: 5.87/3=1.96

In conclusione, la distribuzione che meglio si adatta ai dati sperimentali è quella di Poisson, in quanto presenta il chi-quadro ridotto minore.

Esercizio 2

In tabella sono riportate le misure di due grandezze x e y

X	1.	2.	3.	4.	5.
Y	40.	15.	20.	18.	8.

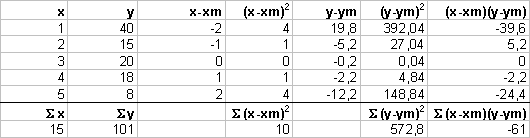
a) Calcolate la covarianza delle due grandezze

b) Calcolate il coefficiente di correlazione lineare

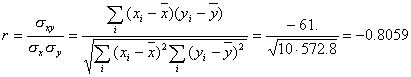
c) Potete escludere, al livello del 5%, che le due grandezze siano incorrelate?

Sulla tabella, in corrispondenza di N=5 e r=0.8 , troviamo il valore 10%

Ma, ricordiamo, questa è la probabilità che 5 misure non correlate diano un coefficiente r più grande di 0.8

Pertanto non è possibile escludere, al livello del 5%, che le misure siano incorrelate, poichè abbiamo ottenuto un valore più grande (10%).

Esercizio 3

I risultati della misura della grandezza q, in tre diversi laboratori, sono :

a) (2.45 ± 0.12) g

b) (2.55 ± 0.05) g

c) (2.5 ± 0.2) g

Esprimete la miglior stima, per il risultato e l’errore della grandezza q, che potete evincere dalle tre misure riportate.

Prima di tutto notiamo che le tre misure sono sicuramente compatibili, in quanto le bande di errore si sovrappongono.
E’ necessario utilizzare le medie pesate, poichè i risultati dei tre laboratori hanno incertezze differenti.

Ora possiamo applicare le formule:

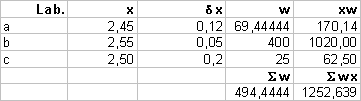
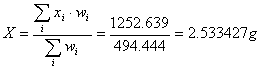
da cui

x=(2.53± 0.04)g