Prova scritta di Fisica – Modulo II – CdL in BIOTECNOLOGIE
AA 2000/2001 – 5 giugno 2001
Prova di esonero n. 2
Prof. G. Sartorelli – Dott. M. Selvi

COMPITO D

Esercizio 1

La frequenza media attesa di decadimenti radioattivi di un certo campione è di 7 s^-1 .

a) Se volessimo effettuare una misura con un’incertezza minore del 5%, per quanto tempo dovremmo contare?
Se ho N conteggi di decadimenti radioattivi, l’incertezza è .

Allora l’errore relativo vale:

Supponiamo ora di effettuare 100 esperimenti e di misurare i seguenti risultati.

frequenza di decadimenti (s^-1)	0	1	2	3	4	5	6	7	8	9
Volte osservate	0	0	4	8	11	15	14	19	16	13

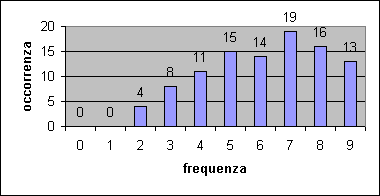
b) Disegnare l’istogramma della distribuzione dei dati ottenuti.

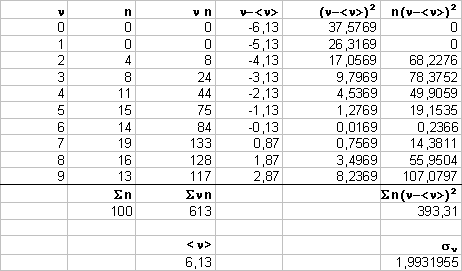
c) Calcolare la media e la dev. standard dai dati ottenuti e confrontarle con i valori attesi.

d) Calcolare, sulla base della media attesa, qual è la probabilità di ottenere una frequenza di 6 s^-1



e) Quante volte ci si aspetta di osservare una frequenza di 3 s^-1 se si compiono 1000 esperimenti.

Eventi attesi:

Esercizio 2

x in mm (dx trascurabile)	2.	4.	6.	8.
N	220	108	41	22

La legge che governa l’assorbimento della radiazione è N(x)=N₀ e ^{-m x} dove x è lo spessore di materiale attraversato, N è il numero di conteggi misurati, N₀ è il numero di conteggi in assenza di materiale e m è il coefficiente di assorbimento tipico del materiale in questione.

a) Disegnare un grafico (ln N, x) con i dati e le incertezze.

b) Utilizzando il metodo grafico, stimare i valori dei parametri N₀ e m che meglio approssimano i dati della tabella e valutare graficamente le incertezze sui parametri.

c) Utilizzando il metodo dei minimi quadrati, calcolare i valori dei parametri N₀ e m che meglio

approssimano i dati della tabella, dopo aver linearizzato la relazione data.
N(x)=N₀ e ^{-m x} ln(N)=ln(N₀)-mx

y=ln(N) A=ln(N₀) B=-m -------> y=A+Bx

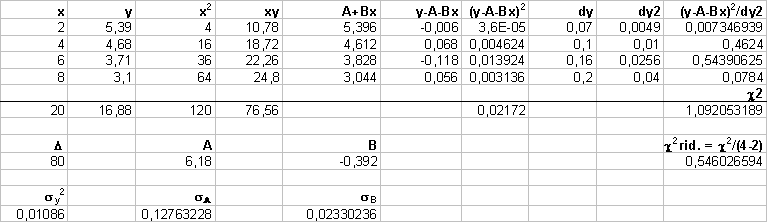
B=(-0,39 ± 0,02) mm^-1 da cui m =(0,39 ± 0,02) mm^-1
A=(6,18 ± 0,13) N₀=e^A = 482,991 dN₀ = e^A dA = 61,64 ˜ 60 da cui N₀ = (480 ± 60)

d) Confrontare i risultati ottenuti con i due metodi.

e) Con i risultati dei minimi quadrati, valutate se dati e risultati sono in accordo, utilizzando il test c²

Il numero di gradi di libertà, in questo caso, è 2. Ci sono infatti 4 punti sperimentali e 2 vincoli (A e B, cioè quei parametri che sono stati ricavati dai dati stessi).

Il chi-quadro ridotto vale 0.54 , cioè minore di 1, quindi predizione teorica e dati sono in accordo.

Esercizio 3

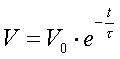La ddp ai capi di un condensatore in scarica dipende dal tempo t secondo la relazione

dove V₀ è noto senza incertezza ed è pari a 9 V R= (100. ± 1.) MW C= (24 ± 1) nF

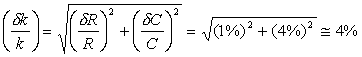a) calcolare il valore e l’incertezza sulla grandezza 1/t , assumendo che le misure di R e C siano indipendenti

Rinomino 1/t = k

dk=0.4166 * 0.04 = 0.01666 da cui k=(0.417 ± 0.017) s^-1

b) calcolare il valore e l’incertezza di V per t = 2s

dove l’incertezza è solo su k.

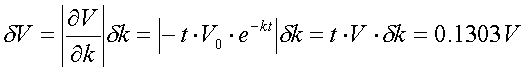
Da cui V = (3.91 ± 0.13) V