Prova scritta di Fisica – Modulo II – CdL in BIOTECNOLOGIE
AA 2000/2001 – 12 giugno 2001
Prof. G. Sartorelli – Dott. M. Selvi

COMPITO A

Esercizio 1

Il numero medio atteso di decadimenti radioattivi di un certo campione è di 2 al minuto.

Supponiamo di effettuare 100 esperimenti, ognuno di un minuto, e di misurare i seguenti risultati.

Numero di decadimenti: n	0	1	2	3	4	5 o più
Volte osservate: n	22	32	25	13	8	0

a)

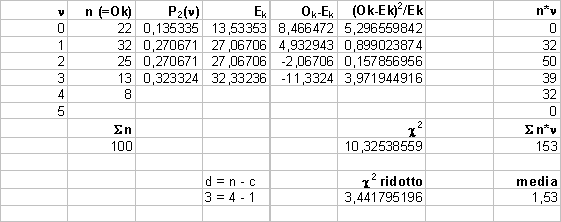
Quali numeri vi attendereste di osservare, nell’ipotesi che i dati seguano una distribuzione di Poisson con media pari a quella attesa. (Raggruppate tutte le osservazioni con n >= 3 in un singolo intervallo)

b) Calcolate il c² ridotto nell’ipotesi del punto a). Quanti sono i gradi di libertà?
c² = S_k [(Ok-Ek)²/Ek] = 10.32
L’unico valore che ricaviamo dai dati, per calcolarci gli Ek, è il numero totale di eventi: quindi i vincoli sono 1. Il numero di gradi di libertà è, quindi, d=n-c=4-1=3
c² ridotto vale 10.32 / 3 = 3.44

c) Al livello del 5%, rigettereste l’ipotesi che il campione segua una distribuzione di Poisson con media pari a quella attesa ?
Dalla tabella ricaviamo che, se dati e teoria fossero in accordo, la probabilità, con 3 gradi di libertà, di ottenere un valore di c² ridotto maggiore o uguale a 3.44 è minore del 2.9%. Pertanto, al livello del 5% rigettiamo l’ipotesi che i dati seguano una distribuzione di Poisson con media 2.

d) Calcolate, dai dati, la media della distribuzione
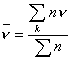= 1.53

Rispondete alle domande dei punti a) b) c), nell’ipotesi che i dati seguano una distribuzione di Poisson con media pari a quella ricavata dai dati.

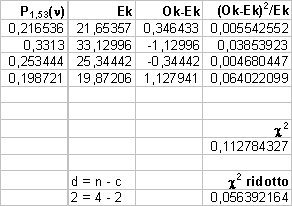
Ora, per calcolare gli Ek, ricaviamo dai dati sia il numero totale di eventi che la media, quindi i vincoli sono 2 e i gradi di libertà sono d = n – v = 4 – 2 = 2
c² ridotto vale 0.11 / 2 = 0.056

E’ molto minore di 1, quindi ci aspettiamo che dati e teoria siano in accordo.
In ogni modo, dalla tabella ricaviamo che, se dati e teoria fossero in accordo, la probabilità, con 2 gradi di libertà, di ottenere un valore di c² ridotto maggiore o uguale a 0.056 è maggiore del 82%. Pertanto, al livello del 5% non rigettiamo l’ipotesi che i dati seguano una distribuzione di Poisson con media 1.53 .

Esercizio 2

La legge che governa la trasformazione adiabatica di un gas perfetto è : P=KV^a

Vengono misurati i seguenti valori (con incertezza trascurabile):

P (kg/cm^2)	603.	228.	129.	87.
V (cm^3)	10.	20.	30.	40.

a) Linearizzare la relazione data
Uso i logaritmi per linearizzare la relazione (non importa in quale base): per es. log. naturali
ln P = ln K + a ln V
pongo y=ln P A=ln K B=a x=ln V
e ottengo y=A+Bx

b) Ricavare, attraverso il metodo dei minimi quadrati, i valori di K e a

c) Calcolare il valore di P quando V = 50 cm³

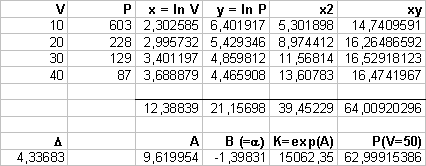
NB: a causa di differenti arrotondamenti o cifre utilizzate potete trovare risultati differenti.

NNBB: non avendovi chiesto di calcolare le incertezze sui parametri, non potete stimare quante cifre significative usare nel risultato, in questo caso dovete riportare tutte quelle che ottenete senza arrotondamenti, spiegando il motivo.

Esercizio 3

Calcolare valore e incertezza della grandezza q = 2x + y lnz

dove x=(200. ± 1.)m y=(12. ± 1.)m z=(100. ± 3.), assumendo che le misure di x, y, e z non siano indipendenti.

q = 2x + y lnz = 2 200 + 12 ln 100 = 455.2620422 m

le misure non sono indipendenti perciò

Risultato: q = (455 ± 7) m

Attenzioni !!!
Le tabelle con i vari calcoli parziali sono obbligatorie

Evidenziate bene il risultato di ogni punto di ogni esercizio (es. 1b, 2c, etc.)